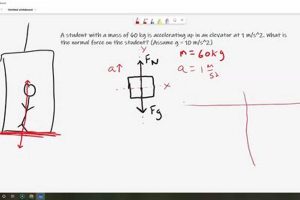
Conceptual misunderstandings and common errors in physics problem-solving are often referred to as stumbling blocks. These can range from misinterpreting fundamental concepts like force, velocity, or energy, to applying incorrect formulas or making mathematical mistakes. For instance, confusing velocity and acceleration or neglecting air resistance in projectile motion are typical examples. Analyzing and addressing these challenges is crucial for developing a robust understanding of physical principles.
Overcoming these challenges is essential for developing a strong foundation in the subject. Historically, identifying and addressing these common pitfalls has been a key aspect of physics education. By understanding where students typically struggle, educators can develop more effective teaching strategies and resources. This focus allows for more efficient learning and helps students develop a deeper, more intuitive understanding of physics. Furthermore, recognizing these challenges can improve critical thinking skills and problem-solving abilities, which are valuable assets in various fields.
This article will further explore specific categories of these conceptual and procedural difficulties, offering practical advice and strategies for effective remediation. Topics to be covered include Newtonian mechanics, electricity and magnetism, and thermodynamics, with a particular emphasis on identifying the root causes of these issues and providing targeted solutions.
Tips for Overcoming Common Physics Challenges
This section offers practical advice for addressing common conceptual and procedural difficulties encountered in physics. Each tip provides specific strategies and examples to facilitate a deeper understanding and improve problem-solving skills.
Tip 1: Visualize Concepts: Abstract concepts can be challenging. Creating diagrams, graphs, or mental images can significantly enhance understanding. For example, visualizing vectors as arrows with magnitude and direction aids in grasping vector addition and subtraction.
Tip 2: Master Fundamental Concepts: A solid grasp of basic principles is crucial. Ensure a clear understanding of concepts like force, energy, and momentum before tackling more complex problems. Review foundational material regularly.
Tip 3: Practice Regularly: Consistent practice is essential for developing proficiency. Working through a variety of problems, from simple to complex, solidifies understanding and builds problem-solving skills.
Tip 4: Check Units and Dimensions: Dimensional analysis serves as a powerful tool for verifying the correctness of equations and calculations. Ensure consistent units throughout calculations to avoid errors.
Tip 5: Break Down Complex Problems: Divide complex problems into smaller, manageable steps. This approach simplifies the problem-solving process and reduces the likelihood of errors.
Tip 6: Seek Clarification When Needed: Don’t hesitate to consult resources or seek assistance when encountering difficulties. Textbooks, online resources, and instructors can provide valuable guidance.
Tip 7: Review Mistakes: Analyzing mistakes provides valuable learning opportunities. Understanding the root cause of errors helps prevent similar mistakes in the future.
By implementing these strategies, one can develop a more robust understanding of physics principles and improve problem-solving proficiency. These tips offer a pathway to navigate common challenges and build a strong foundation in the subject.
The following section will delve into specific examples and case studies illustrating the application of these tips in various physics domains.
1. Conceptual Misunderstandings
Conceptual misunderstandings form a core component of common errors in physics. These misunderstandings represent a flawed or incomplete grasp of fundamental principles, leading to incorrect application of formulas, misinterpretation of physical phenomena, and ultimately, incorrect solutions. A clear example is the confusion between weight and mass. Weight is the force of gravity acting on an object, while mass is an intrinsic property representing the amount of matter. Conflating these concepts can lead to errors in calculations involving forces, momentum, and energy. Another prevalent misunderstanding arises in interpreting Newton’s Third Law of Motion. The law states that for every action, there is an equal and opposite reaction. However, a common misconception is that these action-reaction forces cancel each other out. This is incorrect because the forces act on different objects. Failing to grasp this crucial point can lead to significant errors in analyzing dynamic systems.
The impact of conceptual misunderstandings extends beyond individual problem-solving. These misunderstandings can hinder the ability to build a robust understanding of more complex physics topics. For example, a weak understanding of basic kinematics can impede the ability to grasp more advanced concepts in dynamics, rotational motion, or even quantum mechanics. Furthermore, conceptual misunderstandings can hinder the development of critical thinking skills essential for scientific reasoning. The ability to analyze a problem, identify underlying principles, and apply appropriate concepts is crucial, not only in physics but also in various other scientific disciplines and real-world scenarios. Consider the design of a bridge. A fundamental understanding of forces, stress, and strain is crucial. Conceptual misunderstandings in these areas can lead to structural deficiencies and potentially catastrophic failures.
Addressing conceptual misunderstandings is therefore essential for successful physics learning. This involves not just memorizing formulas but developing a deeper understanding of the underlying principles governing physical phenomena. Utilizing diverse learning strategies, such as visualizations, thought experiments, and real-world applications, can be crucial in overcoming these misunderstandings and building a solid foundation for advanced learning and practical application.
2. Formula Misapplication
Formula misapplication represents a significant category within the broader context of common physics errors. While a formula serves as a concise expression of a physical relationship, its correct application hinges on a clear understanding of the underlying concepts and the specific conditions under which the formula holds true. Misapplication arises from several sources, including a lack of conceptual clarity, incorrect substitution of variables, or overlooking the limitations of the formula’s applicability. Consider, for example, the formula for kinetic energy: KE = 1/2 m v. If one mistakenly substitutes velocity for speed, or uses the formula in a context involving relativistic speeds without appropriate modification, the calculated kinetic energy will be incorrect. Similarly, applying the ideal gas law under conditions of high pressure or low temperature, where the assumptions of ideality break down, leads to inaccurate predictions.
The consequences of formula misapplication extend beyond simply obtaining incorrect numerical answers. It can reinforce conceptual misunderstandings and hinder the development of a robust understanding of physical principles. For instance, consistently misapplying the formula for work done by a force can lead to a flawed understanding of the relationship between work, force, and displacement. This, in turn, can impede the ability to analyze more complex systems involving energy transformations. In practical applications, formula misapplication can have significant real-world consequences. Consider the calculation of braking distance for a vehicle. Using an incorrect formula or substituting incorrect values for parameters like friction coefficient or initial velocity can lead to a gross underestimation of the required stopping distance, potentially resulting in accidents.
Mitigating formula misapplication requires a multi-pronged approach. A strong foundation in fundamental concepts is essential. This includes not just knowing the formula itself but also understanding its derivation, the physical principles it represents, and the limitations of its validity. Careful attention to units and dimensions is also crucial. Dimensional analysis serves as a powerful check against incorrect substitutions and inconsistencies. Finally, consistent practice and critical evaluation of results are indispensable. By working through a variety of problems and scrutinizing the obtained results for reasonableness and consistency, one can refine their understanding and avoid common pitfalls associated with formula misapplication.
3. Mathematical Errors
Mathematical errors constitute a significant source of difficulty in physics problem-solving. While physics principles provide the conceptual framework, mathematics serves as the language for quantifying and analyzing physical phenomena. Consequently, mathematical proficiency is essential for accurate and meaningful application of physics principles. Even a minor mathematical error can lead to substantial deviations from the correct solution, obscuring the underlying physics and hindering progress. This section explores several facets of mathematical errors commonly encountered in physics.
- Arithmetic Errors:
Simple arithmetic mistakes, such as incorrect addition, subtraction, multiplication, or division, can have a cascading effect throughout a problem, leading to an incorrect final answer. These errors are particularly problematic in multi-step calculations where intermediate results are used in subsequent steps. For example, an incorrect calculation of net force due to an arithmetic error will lead to an incorrect value for acceleration, which subsequently affects calculations of velocity and displacement.
- Algebraic Errors:
Algebraic manipulation is frequently required in physics to solve for unknown variables or rearrange equations. Errors in algebraic steps, such as incorrect transposition of terms, improper factoring, or mishandling of exponents and radicals, can lead to incorrect expressions and ultimately, incorrect solutions. An example includes solving for time in a kinematic equation involving quadratic terms where an incorrect algebraic step can lead to incorrect or even non-physical solutions.
- Trigonometric Errors:
Many physics problems involve vector quantities and require trigonometric functions for resolution into components or calculation of angles. Errors in applying trigonometric functions, such as using the wrong function (sine, cosine, tangent) or incorrectly identifying the relevant angle, can lead to incorrect vector components and ultimately, incorrect results. This is common in projectile motion problems where resolving initial velocity into horizontal and vertical components is essential for accurate trajectory analysis.
- Calculus Errors:
Calculus concepts, including differentiation and integration, are fundamental to many areas of physics. Errors in applying calculus, such as incorrect differentiation of a function or improper evaluation of definite integrals, can lead to significant deviations from the correct solution. This is frequently encountered in problems involving rates of change, such as calculating instantaneous velocity from displacement or determining work done by a variable force.
These various mathematical errors are not mutually exclusive and often occur in combination. Addressing these challenges requires a focus on developing mathematical proficiency alongside conceptual understanding in physics. Careful attention to detail, systematic problem-solving approaches, and consistent practice are essential for minimizing mathematical errors and ensuring accurate and meaningful application of physics principles. Overcoming these mathematical hurdles contributes directly to a more robust and accurate understanding of the physical world.
4. Ignoring Assumptions
Ignoring underlying assumptions constitutes a significant source of errors in physics, contributing directly to what can be termed “physics nots”instances where conceptual misunderstandings or procedural missteps lead to incorrect solutions or flawed interpretations of physical phenomena. Assumptions, often implicit, simplify complex systems, making them tractable for analysis. However, overlooking or misinterpreting these assumptions can lead to significant deviations from reality, hindering the accuracy and applicability of physics principles.
- Idealized Models:
Physics frequently employs idealized models, such as point masses, frictionless surfaces, and perfectly elastic collisions. These models simplify calculations but deviate from real-world scenarios. Ignoring the limitations of these idealizationsfor instance, neglecting air resistance when calculating projectile motion over long distancescan lead to substantial inaccuracies. Real-world systems invariably involve complexities not captured by idealized models.
- Boundary Conditions:
Many physics problems involve specific boundary conditions or constraints that define the system’s behavior. Ignoring or misinterpreting these conditions can lead to incorrect solutions. Consider a simple pendulum. The standard formula for its period assumes small angular displacements. Applying this formula to large oscillations, where the small-angle approximation breaks down, results in significant errors. Accurately accounting for boundary conditions is essential for obtaining meaningful results.
- Constant Parameters:
Physics problems often assume certain parameters remain constant, such as gravitational acceleration or the coefficient of friction. However, these parameters may vary in real-world scenarios. For instance, gravitational acceleration changes with altitude. Neglecting this variation can lead to inaccuracies in calculations involving satellite motion or high-altitude projectiles. Understanding the limitations of constant parameter assumptions is crucial for accurate modeling.
- Equilibrium Conditions:
Analyzing systems in equilibrium often involves assumptions about the balance of forces or torques. Ignoring these equilibrium conditions or applying them incorrectly can lead to flawed conclusions about the system’s stability or behavior. Consider a static equilibrium problem involving a ladder leaning against a wall. Neglecting the frictional force at the base of the ladder can lead to an incorrect assessment of its stability. Proper application of equilibrium principles is essential for accurate analysis.
These facets of ignoring assumptions underscore the importance of critically evaluating the underlying simplifications and constraints inherent in physics problems. Recognizing the limitations of idealized models, accounting for boundary conditions, acknowledging the potential variability of parameters, and properly applying equilibrium principles are crucial for avoiding “physics nots” and ensuring accurate, meaningful applications of physics principles to real-world scenarios.
5. Unit Inconsistencies
Unit inconsistencies represent a frequent source of errors in physics, contributing significantly to “physics nots”instances where incorrect calculations or flawed interpretations arise from procedural missteps. Consistent and correct unit usage is paramount for accurate quantitative analysis in physics. Failing to maintain unit consistency throughout calculations or misinterpreting units can lead to nonsensical results and obscure the underlying physical relationships. This section explores the critical connection between unit inconsistencies and erroneous outcomes in physics.
- Mismatched Units in Equations:
Using mismatched units within an equation leads to numerically incorrect and physically meaningless results. For example, adding a quantity expressed in meters to another expressed in kilograms violates fundamental principles of dimensional analysis. Equations must have consistent units on both sides to represent valid physical relationships. Attempting to solve an equation with mismatched units yields a result with no physical significance and contributes directly to erroneous conclusions.
- Incorrect Unit Conversions:
Unit conversions are frequently required in physics problems to ensure compatibility within equations or to express results in desired units. Errors in unit conversion factors or applying incorrect conversion procedures can propagate through calculations, leading to substantial deviations from the correct answer. For instance, failing to convert kilometers per hour to meters per second when using kinematic equations will yield incorrect values for quantities like acceleration or displacement. Accurate unit conversions are crucial for obtaining meaningful results.
- Ignoring Unit Prefixes:
Unit prefixes, such as kilo-, milli-, and micro-, represent scaling factors that modify the base unit. Ignoring or misinterpreting these prefixes can lead to significant errors in calculations. For example, overlooking the “milli” prefix in “millimeter” can result in calculations being off by a factor of one thousand. Careful attention to unit prefixes is essential for accurate numerical analysis.
- Dimensionally Inconsistent Formulas:
Formulas themselves must be dimensionally consistent. Each term in an equation must have the same overall dimensions. Using a formula with dimensionally inconsistent terms inherently leads to incorrect results and indicates a fundamental flaw in the equation’s construction or application. Dimensional analysis serves as a powerful tool for identifying such inconsistencies and ensuring the validity of formulas.
These facets of unit inconsistency highlight the crucial role of accurate unit usage in physics problem-solving. Maintaining consistent units throughout calculations, performing accurate unit conversions, paying close attention to prefixes, and ensuring dimensional consistency in formulas are essential practices for avoiding “physics nots” and obtaining meaningful, physically accurate results. Ignoring these principles can lead to a cascade of errors, obscuring the underlying physics and hindering a robust understanding of the physical world.
Frequently Asked Questions about Common Physics Errors
This section addresses common queries regarding conceptual misunderstandings and procedural errors encountered in physics problem-solving. Clarity on these issues is essential for developing a robust understanding of physical principles and improving problem-solving proficiency.
Question 1: How can conceptual misunderstandings be identified and addressed effectively?
Conceptual misunderstandings often manifest as repeated errors of a similar nature or difficulty in grasping fundamental principles. Addressing these requires focused review of core concepts, utilizing diverse learning resources, and seeking clarification from instructors or peers. Visualizations, thought experiments, and real-world applications can significantly aid in solidifying conceptual understanding.
Question 2: What are common sources of formula misapplication?
Formula misapplication often stems from a lack of clarity regarding the formula’s underlying assumptions, limitations, and the specific conditions under which it holds true. Incorrect substitution of variables, overlooking unit conversions, or using a formula outside its domain of applicability are frequent sources of error.
Question 3: How can mathematical errors be minimized in physics problem-solving?
Minimizing mathematical errors requires a combination of careful attention to detail, systematic problem-solving approaches, and consistent practice. Checking calculations, utilizing dimensional analysis, and breaking down complex problems into smaller, manageable steps can significantly reduce the likelihood of mathematical errors.
Question 4: Why is it important to consider underlying assumptions in physics problems?
Assumptions simplify complex systems, making them tractable for analysis. However, ignoring or misinterpreting these assumptions can lead to significant deviations from reality. Critically evaluating the underlying simplifications and constraints is essential for obtaining accurate and meaningful results.
Question 5: What are the consequences of unit inconsistencies in physics calculations?
Unit inconsistencies lead to numerically incorrect and physically meaningless results. Maintaining consistent units throughout calculations is crucial for obtaining accurate and interpretable solutions. Errors in unit conversions or mismatched units within equations can have significant repercussions on the final outcome.
Question 6: How can one improve overall physics problem-solving skills?
Improving problem-solving skills involves a combination of strengthening conceptual understanding, practicing regularly with diverse problem sets, seeking feedback on solutions, and focusing on developing mathematical proficiency. Utilizing available resources, such as textbooks, online tutorials, and study groups, can further enhance learning and problem-solving capabilities.
Addressing these common concerns regarding conceptual and procedural errors is paramount for developing a strong foundation in physics. This understanding allows for more effective learning and application of physical principles to a wide range of problems and scenarios.
The next section offers specific examples and case studies illustrating these common errors and their impact on physics problem-solving.
Conclusion
This exploration has highlighted the critical role of addressing common pitfalls in physics. Conceptual misunderstandings, formula misapplication, mathematical errors, overlooking assumptions, and unit inconsistencies contribute significantly to incorrect solutions and hinder a robust understanding of physical principles. Recognizing and mitigating these challenges is essential for developing proficiency in problem-solving and building a strong foundation in the subject.
The accurate application of physics principles relies on a multifaceted approach encompassing conceptual clarity, mathematical precision, and a critical awareness of underlying assumptions. Continued focus on these areas is crucial for advancing knowledge, fostering innovation, and effectively applying physics to real-world challenges. Rigorous attention to detail and a commitment to continuous improvement are essential for minimizing errors and achieving accurate, meaningful results in the pursuit of understanding the physical world.