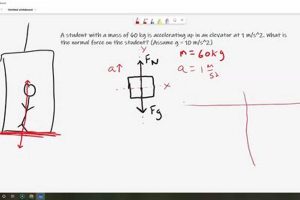
Educational materials focusing on classical mechanics typically include exercises related to the three fundamental principles of motion and gravitation. These exercises often take the form of problem sets requiring calculations, explanations, and the application of core concepts to hypothetical scenarios. For instance, a problem might involve calculating the force required to accelerate an object of a given mass at a specific rate, or predicting the trajectory of a projectile given its initial velocity and angle of launch. These practice activities are essential for developing a concrete understanding of the subject matter.
A deep understanding of these fundamental principles is crucial for numerous fields, from engineering and architecture to space exploration and robotics. These laws provide the framework for understanding how objects interact with forces and move through space. Historically, their formulation marked a turning point in scientific thought, paving the way for modern physics and technological advancements. Developing proficiency in applying these laws allows students to build a strong foundation for more advanced studies in physics and related disciplines.
The following sections will delve deeper into specific applications of these principles, exploring topics such as inertia, momentum, and the relationship between force, mass, and acceleration. Further examples and practice problems will be provided to solidify understanding and demonstrate the practical relevance of these fundamental laws in various contexts.
Tips for Effective Learning with Classical Mechanics Exercises
Maximizing the learning benefits of mechanics problem sets requires a focused and strategic approach. The following tips provide guidance for effectively utilizing these resources to build a strong understanding of fundamental principles.
Tip 1: Diagram the Scenario: Visualizing the problem through a clear diagram helps clarify the forces, motion, and relationships between different objects involved. Include labels and known values.
Tip 2: Identify Known and Unknown Variables: List all given quantities and the desired unknown variables. This helps organize information and select appropriate equations.
Tip 3: Choose Relevant Equations: Carefully select the formulas that connect the known and unknown variables. Ensure the equations align with the specific scenario being analyzed.
Tip 4: Solve Systematically: Substitute known values into the chosen equations and solve step-by-step. Maintain clear units throughout the calculations.
Tip 5: Check Units and Reasonableness: Verify that the units of the final answer are correct and that the magnitude and direction of the result are physically reasonable within the context of the problem.
Tip 6: Review and Reflect: After solving, review the process and identify areas where challenges arose. Reflecting on the solution strategy deepens understanding and improves problem-solving skills.
Tip 7: Consider Limiting Cases: Test the solution by considering extreme scenarios, such as zero mass or zero velocity. The behavior in these limits should align with intuitive expectations.
Consistent application of these strategies cultivates a robust understanding of the underlying principles and fosters proficiency in problem-solving. This approach promotes a deeper grasp of the material and prepares individuals for more advanced studies and applications.
By mastering these core concepts, individuals lay a solid groundwork for further exploration of physics and its applications in diverse fields.
1. Motion Analysis
Motion analysis forms a cornerstone of understanding and applying Newton’s Laws of Motion. Worksheets focused on these laws invariably incorporate motion analysis as a core component. The relationship stems from the need to quantify and explain observed movements in terms of forces and inertia. Cause and effect are directly linked: forces cause changes in motion, and analysis of those changes reveals information about the forces involved. For example, observing an object accelerating downwards allows one to infer the force of gravity acting upon it. Similarly, analyzing the trajectory of a projectile reveals the influence of initial velocity and air resistance.
Within the context of a physical science worksheet, motion analysis often involves calculating displacement, velocity, and acceleration. These calculations may involve interpreting graphs, applying kinematic equations, or analyzing experimental data. A real-world example could involve determining the braking distance of a car based on its initial speed and deceleration rate. Such calculations directly apply Newton’s Second Law, linking force, mass, and acceleration. Understanding motion analysis enables one to predict future motion, a crucial skill in fields like engineering and space exploration. Consider calculating the trajectory adjustments needed for a spacecraft to reach a specific target.
In summary, motion analysis serves as an essential tool for applying and understanding Newton’s Laws. It provides the framework for linking observed motion to the forces responsible. Practical applications range from calculating simple trajectories to designing complex systems. Challenges can arise when multiple forces act simultaneously or when motion occurs in multiple dimensions, requiring more advanced analytical techniques. Nevertheless, the ability to analyze motion remains fundamental to understanding the physical world and applying these fundamental laws of physics effectively.
2. Force Calculations
Force calculations are inextricably linked to any comprehensive exploration of Newton’s Laws of Motion. Within the context of a physical science worksheet, these calculations serve as a primary means of applying and testing comprehension of the laws. This connection stems directly from Newton’s Second Law, which establishes the fundamental relationship between force, mass, and acceleration (F=ma). Force calculations become necessary to quantify the impact of forces on an object’s motion. Cause and effect are explicitly defined: net forces cause acceleration, and the magnitude of that acceleration is determined through calculation. For instance, determining the force required to accelerate a car at a specific rate necessitates applying the second law. Another example involves calculating the gravitational force acting on an object, which relies on the object’s mass and the acceleration due to gravity.
The importance of force calculations within these educational materials is paramount. They transition the laws from abstract concepts to tangible applications. Consider a scenario involving a block sliding down an inclined plane. Calculating the force due to gravity, the normal force, and the frictional force are essential for predicting the block’s motion. Such calculations bridge theoretical principles and practical problem-solving. Furthermore, understanding these calculations enables predictions about real-world events, such as determining the thrust required to launch a rocket or analyzing the forces acting on a bridge. The practical significance extends to engineering, architecture, and any field involving the dynamics of moving objects.
In summary, force calculations are integral to understanding and applying Newton’s Laws. They offer a quantitative framework for analyzing the cause and effect of forces on motion. Practical applications span diverse fields, highlighting the importance of these calculations for problem-solving and predicting real-world phenomena. Challenges can arise when dealing with complex systems involving multiple forces or changing accelerations, necessitating more advanced mathematical tools. However, the ability to perform accurate force calculations remains a cornerstone of comprehending and applying these fundamental principles of physics.
3. Free Body Diagrams
Free body diagrams (FBDs) are indispensable tools within physical science worksheets focused on Newton’s Laws. They provide a visual representation of all forces acting upon an isolated object, facilitating analysis and problem-solving. This visual approach clarifies the interplay of forces, enabling accurate application of Newton’s laws to predict motion or calculate unknown forces. Constructing FBDs is essential for transitioning from conceptual understanding to practical application of the laws.
- Isolation of the Body
The core principle of an FBD is isolating the object of interest from its surroundings. This isolation allows for a focused analysis of forces acting directly on that object, excluding extraneous influences. For example, analyzing a book resting on a table requires isolating the book to consider only gravity and the normal force from the table, ignoring forces acting on the table itself. This isolation clarifies the forces directly influencing the book’s equilibrium.
- Representation of Forces
Forces are represented as vectors on the FBD, indicating both magnitude and direction. The tail of each vector originates at the center of mass of the isolated object. Gravity is always directed downwards, while other forces, like friction or tension, align with their respective sources. For instance, tension in a rope pulling an object is represented by a vector pointing along the rope, away from the object. Accurate vector representation is crucial for correctly applying Newton’s Second Law.
- Coordinate System
A coordinate system provides a reference frame for analyzing the forces. Typically, one axis aligns with the direction of motion or the dominant force. This facilitates decomposition of forces into components, simplifying calculations. For example, when analyzing an object on an inclined plane, aligning one axis parallel to the incline simplifies the representation of gravitational force components. Proper coordinate system selection is vital for accurately resolving forces and applying Newton’s laws.
- Application of Newton’s Laws
Once the FBD is constructed, Newton’s Laws can be applied to solve for unknowns. Newton’s Second Law, in particular, becomes a powerful tool for linking the net force to the object’s acceleration. For instance, if an object is at rest or moving at a constant velocity, the net force, as represented by the vector sum of forces in the FBD, must be zero. This allows for calculation of unknown forces, such as the force of friction required to keep an object stationary on an incline. FBDs thus provide the necessary visual framework for applying the laws and solving real-world problems.
In conclusion, free body diagrams serve as a crucial link between the conceptual understanding of Newton’s Laws and their practical application within physical science worksheets. They provide a structured approach for visualizing forces, simplifying complex scenarios, and enabling accurate application of the laws to solve for unknown forces or predict motion. Mastery of FBD construction is thus fundamental for any student seeking to develop proficiency in classical mechanics.
4. Inertia & Mass
Understanding inertia and mass is fundamental to applying Newton’s Laws of Motion, a core component of any physical science curriculum. Worksheets addressing these laws often dedicate significant attention to the concept of inertia and its direct relationship with mass. This focus stems from Newton’s First Law, which defines inertia as an object’s tendency to resist changes in its state of motion. A clear grasp of this concept is crucial for analyzing and predicting the motion of objects subjected to various forces.
- Mass as a Measure of Inertia
Mass serves as a quantitative measure of an object’s inertia. A larger mass indicates greater resistance to changes in motion. This translates directly to real-world scenarios: a heavier object requires more force to accelerate or decelerate than a lighter object. Within a worksheet context, problems involving varying masses highlight this principle. Calculating the force required to accelerate a truck versus a bicycle underscores how mass influences the relationship between force and motion. This reinforces the concept of inertia as a fundamental property directly related to mass.
- Inertia in Everyday Examples
Everyday experiences provide tangible demonstrations of inertia. The feeling of being pushed back into a car seat during acceleration or the tendency of a grocery cart to continue rolling forward after releasing it exemplifies inertia in action. Incorporating such examples into worksheet problems helps connect theoretical concepts to practical observations. Analyzing these scenarios through the lens of Newton’s First Law strengthens understanding and promotes deeper engagement with the material.
- Inertia and Equilibrium
An object at rest or moving with constant velocity is said to be in equilibrium. This state of equilibrium is directly linked to the concept of inertia. If no net force acts on an object, its inertia maintains its state of motion, whether at rest or at constant velocity. Worksheets exploring equilibrium often incorporate problems requiring the analysis of balanced forces, highlighting the role of inertia in maintaining a steady state. Analyzing scenarios involving suspended objects or objects resting on surfaces reinforces the connection between inertia and equilibrium.
- Inertia in Rotational Motion
The concept of inertia extends to rotational motion as well. An object’s resistance to changes in its rotational speed is known as rotational inertia, also called the moment of inertia. This property depends not only on the object’s mass but also on how that mass is distributed relative to the axis of rotation. While less common in introductory worksheets, exploring rotational inertia lays the groundwork for more advanced topics in physics. Analyzing the spin of a figure skater or the rotation of a wheel introduces the concept of mass distribution influencing rotational motion.
In summary, understanding inertia and its relationship with mass is crucial for comprehending Newton’s Laws of Motion. Physical science worksheets leverage various scenarios, calculations, and real-world examples to solidify this understanding. The exploration of inertia in linear and rotational motion, its connection to equilibrium, and its everyday manifestations form a comprehensive framework for applying these fundamental principles in diverse contexts.
5. Action-Reaction Pairs
Newton’s Third Law of Motion introduces the concept of action-reaction pairs, stating that for every action, there is an equal and opposite reaction. Within the context of a physical science Newton’s laws worksheet, understanding action-reaction pairs is crucial for analyzing interactions between objects. This principle emphasizes that forces always occur in pairs. When one object exerts a force (action) on another, the second object simultaneously exerts an equal and opposite force (reaction) on the first. This reciprocal nature of forces is fundamental to understanding how objects influence each other’s motion. Cause and effect are intertwined: one object’s action is the direct cause of the other object’s reaction. A clear example is a person walking: the foot pushes backward on the ground (action), and the ground simultaneously pushes forward on the foot (reaction), propelling the person forward.
The importance of action-reaction pairs in these worksheets is underscored through various scenarios. Problems often involve identifying the action-reaction pair in a given interaction. Analyzing a collision between two billiard balls, for example, necessitates recognizing that each ball exerts an equal and opposite force on the other during impact. Similarly, understanding how a rocket propels itself upward requires recognizing the action of the rocket expelling hot gases downward and the reaction of the gases pushing the rocket upward. Such examples clarify the application of Newton’s Third Law and the reciprocal nature of forces.
Practical significance of understanding action-reaction pairs extends beyond textbook examples. Designing effective propulsion systems for aircraft or spacecraft relies heavily on this principle. Analyzing the forces involved in everyday activities, such as jumping or swimming, also depends on understanding action-reaction pairs. The concept is fundamental to analyzing any interaction where forces play a role. Challenges arise when identifying the specific objects involved in the interaction. A common misconception involves assuming the action and reaction forces act on the same object, neglecting the crucial distinction that they act on different objects. Clarifying this distinction is key to accurate analysis and problem-solving within the framework of Newton’s Laws.
6. Problem-solving Practice
Problem-solving practice forms the cornerstone of effectively internalizing Newton’s Laws of Motion within a physical science context. Worksheets dedicated to these laws invariably incorporate diverse problem sets, serving as a crucial bridge between theoretical understanding and practical application. Engaging with these problems allows students to test their comprehension, develop analytical skills, and solidify their grasp of the core principles governing motion and forces.
- Varied Problem Types
Problem sets encompass a wide range of scenarios, from simple calculations of force and acceleration to more complex analyses involving multiple forces and changing motion. This variety exposes students to diverse applications of the laws, promoting adaptability and a deeper understanding of the underlying principles. Examples include calculating the trajectory of projectiles, analyzing the motion of objects on inclined planes, and determining the forces involved in circular motion. Each problem type presents unique challenges, fostering critical thinking and problem-solving skills tailored to specific physical scenarios.
- Real-World Applications
Many problems connect Newtonian mechanics to real-world situations, increasing engagement and demonstrating the practical relevance of these fundamental laws. Examples include analyzing the forces involved in car crashes, calculating the optimal angle for launching a basketball, or understanding the principles behind rocket propulsion. These real-world connections provide context and motivate students to apply the laws beyond abstract theoretical frameworks. Such applications highlight the significance of Newtonian mechanics in everyday phenomena and engineering applications.
- Stepwise Approach to Solutions
Effective problem-solving often involves a structured, stepwise approach. This typically includes identifying known and unknown variables, selecting appropriate equations, performing calculations, and checking the reasonableness of results. Worksheets often guide students through this process, fostering methodical problem-solving habits. A structured approach ensures that solutions are derived logically and consistently, reinforcing good analytical practices. This systematic approach promotes clarity and reduces errors in applying the laws to complex scenarios.
- Conceptual Understanding and Mathematical Skills
Problem-solving practice not only reinforces conceptual understanding but also hones mathematical skills essential for applying Newton’s Laws. Calculations involving vectors, trigonometry, and algebra frequently appear in these problem sets, providing opportunities to practice and refine these mathematical tools within a physics context. Strengthening mathematical proficiency ensures that students can effectively translate physical scenarios into mathematical models and accurately solve for unknown quantities, thereby bridging the gap between theory and practice.
In essence, problem-solving practice within physical science Newton’s laws worksheets serves as a crucial training ground for applying and internalizing these fundamental principles. By engaging with diverse problem types, connecting theory to real-world applications, and employing structured problem-solving strategies, students cultivate a deep and robust understanding of Newtonian mechanics, preparing them for more advanced studies and practical applications in various scientific and engineering disciplines.
Frequently Asked Questions
This section addresses common queries regarding the application and understanding of Newton’s Laws of Motion, often encountered when working with related educational materials.
Question 1: How does one differentiate between mass and weight?
Mass represents the amount of matter in an object, while weight represents the force of gravity acting upon that mass. Mass remains constant regardless of location, while weight varies depending on the gravitational field strength.
Question 2: Why doesn’t an object in motion stop immediately when the force applied to it ceases?
Newton’s First Law, the law of inertia, explains this phenomenon. An object in motion tends to stay in motion with the same velocity unless acted upon by a net external force. Friction or air resistance eventually slows and stops the object.
Question 3: How are Newton’s Laws related to momentum?
Newton’s Second Law can be expressed in terms of momentum. The net force acting on an object is equal to the rate of change of its momentum. This relationship is particularly useful in analyzing collisions and other interactions where momentum is conserved.
Question 4: What is the significance of a free body diagram?
Free body diagrams isolate an object and depict all forces acting directly upon it. This visualization simplifies complex scenarios, allowing for accurate application of Newton’s Second Law to determine the object’s acceleration or calculate unknown forces.
Question 5: How does Newton’s Third Law apply to everyday situations?
Newton’s Third Law is evident in numerous daily activities. Walking, jumping, and even the simple act of sitting on a chair involve action-reaction pairs. When one walks, the foot pushes backward on the ground (action), and the ground pushes forward on the foot (reaction), propelling the person forward.
Question 6: What are some common challenges students face when applying Newton’s Laws?
Common challenges include differentiating between mass and weight, understanding the vector nature of forces, correctly identifying action-reaction pairs, and applying the laws to complex scenarios involving multiple forces or changing acceleration. Practice and careful attention to the underlying principles are key to overcoming these challenges.
A thorough understanding of these concepts is crucial for successful application of Newton’s laws to analyze motion, predict outcomes, and solve related problems.
Further exploration may involve investigating the limitations of classical mechanics in extreme conditions such as relativistic speeds or at the subatomic level.
Conclusion
Exploration of educational resources focused on classical mechanics reveals their importance in developing a robust understanding of fundamental physical principles. Analysis of motion, force calculations, free body diagrams, the concepts of inertia and mass, action-reaction pairs, and comprehensive problem-solving practice emerge as crucial components. These elements collectively contribute to a comprehensive framework for applying and internalizing Newton’s Laws of Motion.
Mastery of these concepts equips individuals with the analytical tools necessary for navigating the complexities of the physical world. Continued exploration and application of these principles are essential for advancements in science, engineering, and related fields. A solid foundation in Newtonian mechanics serves as a springboard for further exploration of more advanced topics in physics and provides a framework for understanding the universe’s intricate workings. Deeper investigation and application of these laws will continue to drive technological innovation and expand scientific understanding.