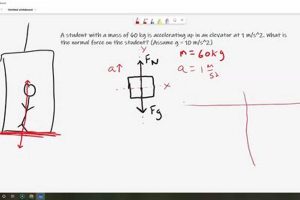
This technique simulates the behavior of physical systems through mathematical equations and algorithms. For instance, simulating the vibration of a guitar string based on its material properties, tension, and length represents an application of this approach. These simulations can often predict how real-world systems will respond to various inputs and conditions.
Simulating system behavior offers significant advantages in design, analysis, and education. It allows for efficient testing and refinement of designs without the need for expensive and time-consuming physical prototypes. Moreover, it facilitates a deeper understanding of the underlying principles governing these systems, enabling advancements in various fields. Historically, its development has been closely tied to advancements in computing power, allowing for increasingly complex and accurate simulations.
The following sections delve into specific applications and further explore the underlying principles, showcasing the breadth and depth of this powerful analytical tool.
Tips for Effective Simulation Development
Developing accurate and efficient simulations requires careful consideration of various factors. The following tips provide guidance for achieving robust and insightful results.
Tip 1: Define Clear Objectives: Begin by precisely defining the goals of the simulation. What specific questions need to be answered? What behaviors need to be predicted? Clearly articulated objectives guide model development and ensure relevant outcomes.
Tip 2: Select Appropriate Software/Tools: Numerous software packages and tools are available, each with its own strengths and limitations. Choosing the right toolset depends on the specific system being modeled and the complexity of the simulation required.
Tip 3: Validate the Model: Model validation is crucial for ensuring accuracy. Compare simulation results against experimental data or known analytical solutions whenever possible. Discrepancies should be investigated and the model refined accordingly.
Tip 4: Simplify When Possible: While complex models can be powerful, unnecessary complexity can lead to computational inefficiencies and obscure key insights. Strive for the simplest model that adequately captures the essential physics.
Tip 5: Document Thoroughly: Maintain comprehensive documentation of the model’s assumptions, parameters, and limitations. This ensures transparency and facilitates future modifications and analyses.
Tip 6: Consider Computational Resources: Complex simulations can require significant computational resources. Assess the available computing power and optimize the model for efficiency to minimize runtime and resource consumption.
Tip 7: Iterate and Refine: Simulation development is an iterative process. Continuously refine the model based on validation results and evolving understanding of the system’s behavior.
By adhering to these guidelines, simulations can become powerful tools for understanding and predicting the behavior of physical systems, leading to more informed decisions and innovative designs.
The subsequent sections provide further details on specific applications and advanced techniques, solidifying the practical value of this approach.
1. Mathematical Representation
Accurate mathematical representation forms the cornerstone of effective physical modeling. Translating physical phenomena into mathematical equations allows for systematic analysis and prediction of system behavior. This process bridges the gap between abstract concepts and quantifiable predictions, enabling deeper understanding and manipulation of the physical world.
- Governing Equations:
Fundamental physical laws, expressed as mathematical equations, govern the behavior of systems. For example, Newton’s laws of motion describe the relationship between force, mass, and acceleration, providing a framework for modeling mechanical systems. Selecting the appropriate governing equations is crucial for capturing the essential physics of the target system. Examples include Navier-Stokes equations for fluid flow, Maxwell’s equations for electromagnetism, and heat transfer equations for thermal analysis.
- Constitutive Relations:
These mathematical relationships describe the specific material properties relevant to the simulation. For instance, the stress-strain relationship of a material dictates how it deforms under load. Accurately representing these properties is essential for predicting realistic system responses. Examples include Hooke’s law for elastic materials, viscosity models for fluids, and thermal conductivity for heat transfer.
- Boundary Conditions:
These define the constraints and interactions of the system with its surroundings. They specify the conditions at the edges or boundaries of the system, such as prescribed temperatures, forces, or displacements. Properly defining boundary conditions ensures that the simulation accurately reflects the real-world operating environment.
- Numerical Discretization:
Continuous mathematical equations are often converted into discrete forms suitable for numerical computation. Techniques like finite element analysis and finite difference methods divide the system into smaller elements or nodes, allowing for approximate solutions. The choice of discretization method impacts the accuracy and computational cost of the simulation.
These interconnected mathematical components, when integrated effectively, provide a powerful framework for simulating and understanding complex physical systems. The accuracy and fidelity of the simulation depend heavily on the appropriate selection and implementation of these mathematical representations, enabling insightful analysis and informed decision-making in various scientific and engineering disciplines.
2. Algorithmic Implementation
Algorithmic implementation translates the mathematical representation of a physical system into a computational model. This crucial step bridges the gap between theoretical formulations and practical simulations. Algorithms provide the step-by-step procedures that computers use to solve the governing equations and predict system behavior. The choice of algorithm significantly impacts the accuracy, efficiency, and stability of the simulation. For instance, explicit methods offer computational simplicity but may be subject to stability limitations, while implicit methods tend to be more stable but computationally demanding. In simulating fluid dynamics, algorithms might discretize the Navier-Stokes equations, transforming them into a system of algebraic equations solvable by computers. In structural mechanics, algorithms could implement finite element analysis, dividing a complex structure into smaller, manageable elements for stress and strain calculations.
The effectiveness of algorithmic implementation relies heavily on several factors. Computational efficiency is paramount, especially for complex simulations involving large datasets or intricate geometries. Algorithms must be optimized to minimize runtime and resource consumption. Accuracy is equally critical. The chosen algorithm must faithfully represent the underlying physics and provide reliable predictions. Stability, particularly in time-dependent simulations, ensures that the solution does not diverge or exhibit spurious oscillations. The selection of an appropriate algorithm depends on the specific characteristics of the physical system being modeled, the desired level of accuracy, and available computational resources. Simulating the trajectory of a projectile requires different algorithmic considerations compared to modeling the complex interactions within a nuclear reactor.
Robust algorithmic implementation is fundamental for leveraging the power of physical modeling. It enables researchers and engineers to explore complex phenomena, test hypotheses, and optimize designs in a virtual environment. Challenges remain in developing efficient and accurate algorithms for increasingly complex systems. However, ongoing advancements in computational methods and hardware continue to expand the horizons of physical modeling, enabling deeper insights into the physical world and driving innovation across various disciplines.
3. System Behavior Prediction
System behavior prediction forms the core purpose of physical modeling. The ability to anticipate how a system will respond under various conditions provides invaluable insights for design, analysis, and control. This predictive capability arises from the mathematical representation and algorithmic implementation inherent in physical models. By simulating the governing equations and boundary conditions, these models generate predictions of system behavior under different scenarios. For instance, in aerospace engineering, predicting the aerodynamic performance of an aircraft wing under varying wind speeds and angles of attack is crucial for optimizing its design and ensuring flight safety. Similarly, in climate modeling, predicting long-term temperature changes based on greenhouse gas emissions allows for informed policy decisions and mitigation strategies.
The accuracy of system behavior prediction relies heavily on the fidelity of the physical model. Factors such as the accuracy of the governing equations, the precision of the numerical methods employed, and the completeness of the input data all contribute to the reliability of the predictions. Model validation, through comparison with experimental data or established analytical solutions, plays a vital role in assessing and improving predictive accuracy. In structural engineering, comparing the predicted deflection of a bridge under load with experimental measurements validates the model and provides confidence in its predictive capabilities. Furthermore, uncertainty quantification techniques help assess the potential range of predicted outcomes, accounting for uncertainties in input parameters and model assumptions.
The practical significance of accurate system behavior prediction extends across numerous domains. From optimizing the performance of engineered systems to understanding complex natural phenomena, physical models offer powerful tools for informed decision-making. In the automotive industry, predicting crashworthiness through simulations helps improve vehicle safety and reduce the need for costly physical crash tests. In meteorology, predicting hurricane paths based on atmospheric models enables timely evacuations and disaster preparedness. Challenges remain in improving the accuracy and efficiency of system behavior prediction, particularly for highly complex systems. However, continued advancements in computational methods and increased availability of data promise to further enhance the predictive power of physical models, leading to deeper understanding and more effective control of physical systems.
4. Model Validation
Model validation is an indispensable component of physical modeling, ensuring the reliability and trustworthiness of simulation results. It represents a critical process of assessing the accuracy and credibility of a computational model by comparing its predictions against experimental data, analytical solutions, or other established benchmarks. This process establishes a direct link between the simulated world and the physical reality it aims to represent. Without rigorous validation, simulation results remain hypothetical and potentially misleading. For example, in designing a bridge, validating a finite element model against strain gauge measurements from a physical scale model ensures the reliability of stress predictions for the full-scale structure. Similarly, in pharmaceutical development, validating a computational model of drug absorption against clinical trial data ensures the model’s predictive power for dosage optimization.
Effective model validation requires a multi-faceted approach. Comparison with experimental data provides a direct measure of model accuracy, highlighting any discrepancies between simulated and observed behavior. Agreement between model predictions and experimental results builds confidence in the model’s ability to represent the physical system. However, experimental data may be limited by practical constraints or measurement uncertainties. Therefore, analytical solutions, derived from simplified representations of the system, offer valuable validation benchmarks, particularly for fundamental physical principles. For instance, validating a fluid flow model against analytical solutions for laminar flow in a pipe provides a baseline assessment of its accuracy. Furthermore, comparing model predictions against established empirical correlations or industry standards offers additional validation avenues, strengthening the model’s credibility. Choosing appropriate validation metrics, such as root-mean-square error or correlation coefficients, quantifies the agreement between model predictions and validation data, providing objective measures of model performance.
Rigorous model validation is essential for ensuring the practical utility of physical modeling. It instills confidence in simulation results, enabling informed decision-making in various fields. From optimizing engineering designs to predicting complex natural phenomena, validated models provide reliable insights and guide effective action. However, challenges remain in validating models of highly complex systems, where experimental data may be scarce or analytical solutions unavailable. Nonetheless, ongoing advancements in experimental techniques and computational methods continue to improve model validation practices, enhancing the trustworthiness and predictive power of physical models across diverse disciplines.
5. Real-world application
The practical value of physical modeling lies in its real-world applications. Bridging the gap between theoretical concepts and tangible outcomes, these applications demonstrate the power and versatility of this approach. From optimizing engineering designs to predicting complex natural phenomena, physical modeling provides invaluable insights and drives innovation across diverse disciplines. The following examples showcase its transformative potential.
- Engineering Design:
Physical modeling plays a crucial role in optimizing engineering designs across various industries. In aerospace engineering, computational fluid dynamics simulations predict the aerodynamic performance of aircraft wings, enabling engineers to optimize lift and drag characteristics. In structural engineering, finite element analysis predicts the stress and strain distribution in bridges and buildings under load, ensuring structural integrity and safety. These simulations reduce the need for expensive and time-consuming physical prototypes, accelerating the design process and fostering innovation.
- Scientific Discovery:
Physical models serve as powerful tools for scientific discovery, enabling researchers to explore complex natural phenomena and test hypotheses in a virtual environment. In astrophysics, simulations of galaxy formation and evolution provide insights into the large-scale structure of the universe. In climate science, global climate models predict long-term temperature changes based on greenhouse gas emissions, informing policy decisions and mitigation strategies. These simulations provide a virtual laboratory for exploring phenomena that are difficult or impossible to study directly.
- Medical Applications:
Physical modeling finds increasing applications in the medical field, contributing to advancements in diagnosis, treatment, and drug development. In biomechanics, simulations of joint movement and tissue deformation aid in the design of prosthetic implants and rehabilitation strategies. In pharmacokinetics, models of drug absorption and distribution predict drug efficacy and optimize dosage regimens. These simulations contribute to personalized medicine and improved patient outcomes.
- Environmental Management:
Physical models play a vital role in environmental management, providing insights for sustainable resource utilization and pollution control. In hydrology, simulations of groundwater flow predict the impact of pumping wells on aquifer depletion. In air quality modeling, simulations predict the dispersion of pollutants from industrial sources, informing emission control strategies and protecting public health. These applications contribute to informed environmental decision-making and sustainable development.
These diverse real-world applications demonstrate the transformative impact of physical modeling. By providing a virtual platform for experimentation and analysis, these models empower engineers, scientists, and researchers to tackle complex challenges, drive innovation, and shape a better future. As computational resources continue to advance and modeling techniques become increasingly sophisticated, the scope and impact of real-world applications of physical modeling will continue to expand, unlocking new possibilities across various disciplines.
Frequently Asked Questions
This section addresses common inquiries regarding the utilization and capabilities of this computational approach.
Question 1: How does computational cost scale with model complexity?
Computational cost typically increases with model complexity. More intricate models require greater computational resources and longer simulation times. Factors influencing computational cost include the number of degrees of freedom, the size of the computational domain, and the complexity of the governing equations.
Question 2: What are the limitations of this methodology?
While powerful, this methodology relies on simplifications and approximations of real-world systems. Model accuracy is limited by the fidelity of the mathematical representation, the accuracy of input data, and the inherent limitations of computational methods. Validation against experimental data or analytical solutions is crucial for assessing model reliability.
Question 3: How does one choose appropriate software or tools?
Selecting appropriate software or tools depends on the specific application and the complexity of the physical system. Factors to consider include the type of physics being modeled, the desired level of accuracy, available computational resources, and the user’s expertise. Different software packages offer specialized capabilities and functionalities tailored to specific domains.
Question 4: What is the role of experimental data in the process?
Experimental data plays a crucial role in validating and refining computational models. Comparing simulation results against experimental measurements assesses model accuracy and identifies areas for improvement. Experimental data also provides essential input parameters for model calibration and initialization.
Question 5: How can model accuracy be improved?
Model accuracy can be improved through various strategies. Refining the mathematical representation by incorporating more detailed physics, using higher-order numerical methods, and employing finer computational grids can enhance accuracy. Validating the model against experimental data and iteratively refining its parameters also contribute to improved accuracy. Additionally, uncertainty quantification techniques assess the potential range of predicted outcomes.
Question 6: What are the future directions of this field?
The field of physical modeling is constantly evolving. Future directions include developing more efficient and accurate algorithms, incorporating machine learning techniques for model calibration and optimization, and integrating multi-physics simulations to capture the complex interactions between different physical phenomena. Advancements in computational resources and experimental techniques will further expand the capabilities and applications of this field.
Understanding these frequently asked questions provides a foundation for effectively utilizing physical modeling for insightful analysis, reliable predictions, and informed decision-making across various disciplines.
The subsequent sections delve into specific applications and advanced techniques, further elucidating the practical utility and transformative potential of this computational approach.
Conclusion
This exploration has highlighted the multifaceted nature of physical modeling, encompassing its mathematical foundations, algorithmic implementation, predictive capabilities, validation processes, and diverse real-world applications. From engineering design and scientific discovery to medical advancements and environmental management, this approach offers invaluable insights and drives innovation across various disciplines. The ability to simulate complex systems in a virtual environment empowers researchers and practitioners to test hypotheses, optimize designs, and predict system behavior under various conditions, leading to informed decision-making and transformative solutions.
As computational resources continue to advance and modeling techniques become increasingly sophisticated, the potential of physical modeling to address complex challenges and shape a better future remains immense. Continued development and refinement of these techniques promise to unlock new possibilities and deeper understanding of the physical world, fostering innovation and driving progress across a wide range of fields. Further exploration and application of these powerful tools are crucial for tackling the complex challenges facing society and shaping a sustainable future.