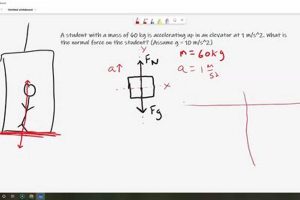
The analysis of systems involving pulleys forms a cornerstone of classical mechanics. These systems, often involving ropes, strings, and multiple interconnected pulleys, serve as excellent models for understanding concepts like tension, force, work, and energy conservation. A simple example involves lifting a heavy object with a single pulley to reduce the required input force. More complex arrangements can achieve significant mechanical advantages, allowing for the lifting of very heavy weights with comparatively little effort.
Studying such mechanical systems provides valuable insights into the principles governing motion and equilibrium. Historically, pulley systems have played crucial roles in engineering and construction, enabling the erection of monumental structures and facilitating heavy lifting long before the advent of modern machinery. Their continued relevance in physics education stems from their ability to illustrate fundamental principles in a tangible way, bridging the gap between abstract theory and practical application. Developing proficiency in analyzing these systems strengthens problem-solving skills applicable to a wide range of engineering and physics-related disciplines.
This exploration will delve into various types of pulley systems, ranging from simple configurations to more complex arrangements. It will cover methodologies for calculating mechanical advantage, analyzing tension within the ropes, and determining the forces acting on each component. Furthermore, the connection between these mechanical principles and broader concepts like energy conservation will be examined.
Tips for Solving Pulley Problems
Approaching pulley problems strategically simplifies the process of finding solutions. The following tips offer guidance for effective analysis and accurate calculations.
Tip 1: Isolate the System: Clearly define the system’s boundaries. Identify all the masses, pulleys, and ropes involved. This clarifies which forces are internal and which are external to the system.
Tip 2: Draw Free-Body Diagrams: Represent each mass and pulley with a separate free-body diagram. Carefully depict all forces acting on each element, including tension, gravity, and normal forces.
Tip 3: Apply Newton’s Second Law: For each mass, apply Newton’s second law (F=ma) in the appropriate directions. Consider the acceleration of each mass and the direction of the net force.
Tip 4: Consider the Rope’s Properties: Assume the rope is massless and inextensible unless otherwise stated. This implies constant tension throughout the rope and equal acceleration for connected masses.
Tip 5: Account for Pulley’s Properties: Consider whether the pulleys are massless and frictionless. Massless, frictionless pulleys only redirect force; they do not change the magnitude of tension in the rope.
Tip 6: Establish Relationships between Accelerations: In systems with multiple connected masses, determine the relationships between the accelerations of each mass. These relationships often depend on the configuration of the pulleys.
Tip 7: Solve the System of Equations: The free-body diagrams and Newton’s second law application will yield a system of equations. Solve this system to determine unknown forces, tensions, and accelerations.
By implementing these strategies, one can effectively analyze pulley systems, determine the forces at play, and predict the motion of the components involved. These methods form a robust framework for tackling even complex pulley configurations.
This foundation in problem-solving techniques prepares for the subsequent exploration of specific examples and advanced concepts within pulley mechanics.
1. Forces
Force analysis forms the bedrock of understanding pulley systems. Within these systems, forces manifest in various forms, primarily as tension in ropes and the gravitational force acting on masses. The interplay of these forces determines the system’s equilibrium or acceleration. A crucial aspect is the tension within the rope, which transmits force from the applied effort to the load being lifted. In an idealized, frictionless system, this tension remains constant throughout the rope. Gravitational force, proportional to the mass of each object in the system, acts downwards, influencing the overall behavior and equilibrium conditions. The vector sum of these forces dictates the net force and subsequent acceleration of each component within the pulley system. For example, in a simple Atwood machine, the difference in gravitational forces acting on the two hanging masses results in a net force and acceleration of the system.
Analyzing these forces allows for prediction and control of system behavior. Understanding tension distribution helps determine the load-lifting capacity of a pulley system, while knowledge of gravitational forces informs the required input effort. Practical applications extend to various fields, including construction, where crane systems utilize pulley principles to lift heavy materials. In elevators, tension and counterweights provide controlled vertical movement. Even in seemingly simpler contexts like raising a flagpole, the underlying principles of force balance and tension play a key role. The absence of force analysis renders understanding the functional principles of these systems impossible. Quantitative analysis involving free-body diagrams and Newton’s laws allows for precise determination of tensions, accelerations, and required forces in various scenarios.
Mastering force analysis in pulley systems offers a foundation for grasping more complex mechanical concepts. This understanding lays the groundwork for exploring work, energy, and power within these systems. Furthermore, it provides a framework for tackling more challenging scenarios involving friction, non-ideal ropes, and complex pulley arrangements. Challenges in force analysis often arise from incorrectly identifying all acting forces or misunderstanding tension transmission. Overcoming these challenges requires diligent application of free-body diagrams and careful consideration of Newton’s laws. This mastery translates into effective problem-solving and the ability to design and analyze a wider range of mechanical systems.
2. Tension
Tension plays a crucial role in the analysis of pulley systems. It represents the force transmitted through a rope, string, or cable when it is pulled tight by forces acting from opposite ends. Understanding tension is fundamental to solving physics pulley problems, as it directly influences the forces acting on the objects within the system and their subsequent motion.
- Constant Tension in Ideal Ropes
In idealized pulley problems, ropes are often considered massless and inextensible. This simplification implies that the tension remains constant throughout the length of the rope. This constant tension transmits the applied force from one end of the rope to the other, facilitating the movement or lifting of objects. For example, in a simple pulley system used to lift a weight, the tension in the rope is equal to the force applied to the rope and also equal to the weight being lifted (ignoring friction). This principle allows for the efficient redirection of force in various mechanical systems.
- Tension and Newton’s Laws
Tension is intrinsically linked to Newton’s laws of motion. When analyzing free-body diagrams of objects in a pulley system, tension forces must be accounted for. These tension forces contribute to the net force acting on each object, which, according to Newton’s second law, determines the object’s acceleration. For instance, in an Atwood machine with two unequal masses connected by a rope over a pulley, the difference in tensions acting on each mass dictates the system’s acceleration. Correctly identifying and calculating tension forces is essential for accurate dynamic analysis.
- Tension and Mechanical Advantage
The concept of mechanical advantage in pulley systems directly relates to the distribution of tension. By increasing the number of rope segments supporting a load, the required input force to lift that load decreases proportionally. This reduction in force is achieved by distributing the load’s weight across multiple sections of rope, each carrying a fraction of the total tension. Consequently, complex pulley systems can lift heavy objects with relatively small input forces, demonstrating the practical application of tension manipulation in achieving mechanical advantage.
- Tension in Real-World Scenarios
While idealized pulley problems assume constant tension and massless ropes, real-world scenarios introduce complexities. Factors such as friction and the elasticity of the rope can influence tension distribution. In these cases, tension might not be uniform throughout the rope’s length. Understanding these factors is crucial for accurate modeling and analysis of real-world pulley systems, including elevators, cranes, and other lifting mechanisms where rope properties and frictional forces play significant roles.
Understanding tension as a force transmitted through ropes and its relationship with Newton’s Laws and mechanical advantage provides a critical foundation for analyzing pulley systems. By correctly accounting for tension forces in free-body diagrams and applying Newton’s laws, one can effectively solve physics pulley problems and gain a deeper understanding of the principles governing these systems. Further exploration can delve into more complex scenarios incorporating friction, elasticity, and real-world constraints, expanding upon this foundational understanding of tension in pulley mechanics.
3. Acceleration
Acceleration, the rate of change of velocity, holds a central position in the analysis of pulley systems. Understanding how forces influence the acceleration of masses within a pulley system is crucial for predicting the system’s dynamic behavior. This involves considering the interplay of tensions, gravitational forces, and the constraints imposed by the pulley configuration. A thorough understanding of acceleration provides insights into the functionality of various mechanical systems and engineering designs based on pulley principles.
- Relationship with Newton’s Second Law
Newton’s second law (F=ma) forms the cornerstone for calculating acceleration in pulley systems. The net force acting on each mass within the system, determined by the vector sum of tension and gravitational forces, directly dictates its acceleration. This principle highlights the direct proportionality between net force and acceleration, with mass acting as the proportionality constant. In pulley systems, the interconnected nature of the masses necessitates considering the constraints on their motion, leading to interconnected accelerations.
- Constraints on Motion and Acceleration
The configuration of pulleys introduces constraints on the motion and, consequently, the acceleration of the masses. In a simple Atwood machine, the two masses connected by a string over a single pulley experience accelerations of equal magnitude but opposite direction. More complex pulley systems with multiple ropes and pulleys introduce more intricate relationships between the accelerations of the connected masses. Analyzing these constraints is essential for accurately determining individual accelerations within the system.
- Impact of Mass Distribution
The distribution of mass within the system significantly influences the resulting acceleration. In an Atwood machine, an imbalance in the masses leads to an acceleration, with the heavier mass accelerating downwards and the lighter mass accelerating upwards. The magnitude of this acceleration depends on the difference in masses and the total mass of the system. Understanding this relationship allows for predicting how variations in mass distribution affect the system’s dynamic response.
- Acceleration and Mechanical Advantage
While mechanical advantage reduces the required input force to lift a load, it correspondingly affects the acceleration of the load. A higher mechanical advantage, achieved through more complex pulley arrangements, results in a lower acceleration of the load for a given input force. This inverse relationship reflects the conservation of energy within the system: a reduced input force necessitates a longer displacement to achieve the same amount of work, resulting in a lower rate of change of velocity, hence a lower acceleration.
By understanding the relationship between acceleration, forces, and constraints in pulley systems, one gains a comprehensive insight into the dynamics of these systems. This understanding provides a foundation for analyzing more complex mechanical systems and optimizing their design for specific applications. Further exploration of friction, energy considerations, and rotational motion of pulleys can enhance this foundation and provide a more nuanced understanding of real-world pulley systems.
4. Work
The concept of work provides crucial insights into the energy transfer within pulley systems. Work, defined as the product of force and displacement in the direction of the force, helps quantify the energy expended in lifting a load using a pulley system. Analyzing work done in pulley systems clarifies the relationship between applied force, displacement, and the energy exchange occurring within the system. This understanding is essential for evaluating the efficiency and mechanical advantage of various pulley configurations.
- Work Done by Applied Force
The work done by the applied force on a pulley system represents the energy input into the system. This work is calculated by multiplying the applied force by the distance the rope is pulled. In an ideal, frictionless pulley system, this work directly translates to the increase in potential energy of the lifted load. Understanding this relationship is essential for determining the energy requirements for lifting a specific load using a given pulley configuration.
- Work Done against Gravity
As a load is lifted within a pulley system, work is done against the force of gravity. This work corresponds to the increase in the load’s gravitational potential energy. The amount of work done against gravity is calculated by multiplying the weight of the load by the vertical distance it is lifted. In an ideal pulley system, the work done by the applied force equals the work done against gravity. This equivalence demonstrates the principle of conservation of energy within the system.
- Work and Mechanical Advantage
Mechanical advantage in a pulley system affects the relationship between work input and output. While a higher mechanical advantage reduces the required input force, it necessitates a proportionally longer displacement of the rope to lift the load to the same height. Consequently, the work done by the applied force remains equal to the work done against gravity, regardless of the mechanical advantage. This highlights the trade-off between force and displacement in pulley systems: reducing force requires increasing displacement to achieve the same amount of work.
- Work in Real-World Pulley Systems
In real-world pulley systems, factors like friction introduce energy losses. This means that the work done by the applied force is greater than the work done against gravity. The difference represents the energy dissipated due to friction, typically converted into heat. Accounting for these losses is crucial for accurate analysis and design of practical pulley systems, such as those used in construction cranes or elevators, where efficiency and energy consumption are critical considerations.
Analyzing work done in pulley systems provides crucial insights into the energy transfer and efficiency of these systems. By understanding the interplay between work, force, displacement, and mechanical advantage, one can effectively evaluate and optimize pulley systems for various applications. Further exploration can consider more complex scenarios involving friction, variable forces, and the rotational work done on the pulleys themselves, offering a more comprehensive understanding of real-world pulley systems.
5. Energy
Energy considerations are fundamental to a complete understanding of pulley systems. Analyzing energy transformations and conservation principles provides insights into the efficiency and limitations of these systems. This involves examining how different forms of energy, primarily potential and kinetic, interact and transform within the system, ultimately influencing the system’s overall behavior.
- Potential Energy
Gravitational potential energy plays a significant role in pulley systems. As a load is lifted, its gravitational potential energy increases proportionally to the height it is raised. This energy is stored within the system due to the object’s position within the Earth’s gravitational field. In a simple pulley system lifting a mass, the work done by the applied force is converted into the increased gravitational potential energy of the mass. This energy transformation is central to understanding how pulleys facilitate the lifting of heavy objects.
- Kinetic Energy
Kinetic energy, the energy of motion, becomes relevant when considering moving components within a pulley system. As a load accelerates, its kinetic energy increases proportionally to the square of its velocity. In a system with moving masses, the interplay between potential and kinetic energy governs the system’s dynamics. For example, in an Atwood machine, the heavier mass loses potential energy as it descends, which is converted into both the increasing kinetic energy of both masses and the increasing potential energy of the lighter mass. Analyzing kinetic energy changes is essential for understanding the system’s acceleration and velocity profiles.
- Conservation of Energy
The principle of conservation of energy states that energy cannot be created or destroyed, only transformed from one form to another. In an ideal, frictionless pulley system, the total mechanical energy, which is the sum of potential and kinetic energy, remains constant. This means that the work done by the applied force is fully converted into the increased potential and kinetic energy of the system. This principle provides a powerful tool for analyzing pulley systems and predicting their behavior, especially in scenarios involving changes in velocity and height.
- Energy Losses in Real Systems
Real-world pulley systems inevitably experience energy losses due to factors like friction within the pulley bearings and air resistance. These losses manifest as heat, reducing the system’s overall efficiency. The work done by the applied force is then not entirely converted into useful potential or kinetic energy but partially dissipated. Accounting for these energy losses is crucial for accurate modeling and design of practical pulley systems. Considerations for minimizing friction and other dissipative forces are vital in optimizing the efficiency of these systems.
Analyzing energy within pulley systems provides a comprehensive understanding of the system’s capabilities and limitations. By considering energy transformations, conservation principles, and potential energy losses, one gains a deeper appreciation for the interplay between forces, motion, and energy within these systems. This understanding forms a solid basis for tackling more complex mechanical systems and addressing real-world engineering challenges.
6. Mechanical Advantage
Mechanical advantage (MA) represents a crucial concept in analyzing pulley systems, quantifying the force amplification achieved by using pulleys. It signifies the ratio of the output force (the weight of the load being lifted) to the input force (the effort applied to the rope). In essence, mechanical advantage describes how much easier it becomes to lift a load using a pulley system compared to lifting it directly. Understanding mechanical advantage is fundamental to designing and optimizing pulley systems for various applications, ranging from simple lifting tasks to complex machinery. The core principle lies in distributing the load force across multiple rope segments, reducing the required input force proportionally.
In a simple pulley system, a single rope loop supports the load, resulting in a mechanical advantage of one. This implies no force multiplication but rather a change in the direction of the applied force. However, in more complex systems involving multiple pulleys and rope segments, the mechanical advantage can be significantly greater than one. For instance, in a system where four rope segments support the load, the input force required is only one-fourth of the load’s weight, resulting in a mechanical advantage of four. This force reduction comes at the expense of increased displacement; the rope must be pulled four times the distance the load is lifted. Real-world examples include crane systems used in construction and elevators where multiple pulleys and cables create substantial mechanical advantages, enabling the lifting of heavy loads with manageable input forces.
The relationship between mechanical advantage and the number of supporting rope segments provides a practical approach to analyzing pulley problems. Identifying the number of rope sections directly supporting the load allows for a straightforward calculation of the mechanical advantage, which in turn simplifies the determination of required forces and potential accelerations within the system. Challenges arise when friction and the weight of pulleys become significant, reducing the effective mechanical advantage. Nevertheless, understanding mechanical advantage remains pivotal in designing efficient lifting systems and provides fundamental insights into the force-displacement trade-off inherent in pulley mechanics. This principle connects directly to the broader themes of work and energy conservation, emphasizing the importance of mechanical advantage in practical applications and real-world engineering contexts.
Frequently Asked Questions
This section addresses common queries regarding the analysis and understanding of pulley systems, aiming to clarify potential misconceptions and reinforce key concepts.
Question 1: How does one determine the mechanical advantage of a complex pulley system?
The mechanical advantage of a pulley system is often (but not always) equal to the number of rope segments directly supporting the load. Careful observation of the rope configuration and how it supports the weight is crucial for accurate determination. However, this rule simplifies a complex concept and may have exceptions. A more rigorous approach involves analyzing the tension distribution throughout the system.
Question 2: What is the role of friction in real-world pulley systems?
Friction within pulley bearings and between the rope and pulley introduces energy losses, reducing the system’s overall efficiency. This means the actual mechanical advantage achieved is lower than the theoretical value calculated based on the number of supporting ropes. Friction converts some of the input work into heat, diminishing the effective force transmitted to the load.
Question 3: Why is the tension assumed constant in idealized pulley problems?
The assumption of constant tension simplifies analysis by neglecting the rope’s mass and elasticity. In such idealized scenarios, the tension throughout the rope is considered uniform. This simplification facilitates clearer understanding of core principles without the added complexity of variable tension.
Question 4: How do Newton’s laws apply to pulley systems?
Newton’s second law (F=ma) is central to analyzing the motion of masses within a pulley system. The net force on each mass, considering tension and gravitational forces, determines its acceleration. Newton’s third law (action-reaction) explains how tension transmits force between connected masses.
Question 5: What is the significance of the work-energy theorem in pulley systems?
The work-energy theorem provides a framework for understanding energy transformations within pulley systems. It states that the net work done on an object equals its change in kinetic energy. This allows for relating the work done by applied forces and against gravity to the changes in kinetic and potential energy within the system.
Question 6: How does one approach pulley problems involving inclined planes?
Pulley problems involving inclined planes require careful consideration of the component of gravity acting parallel to the incline. This component influences the tension in the rope and the acceleration of the masses. Free-body diagrams and resolving forces into components are crucial for analyzing such systems.
These frequently asked questions highlight several critical aspects of pulley mechanics, emphasizing the importance of considering factors such as friction, the idealizations made in theoretical analyses, and the application of fundamental physics principles.
Moving forward, further exploration of specific problem-solving strategies and examples will solidify the understanding of these concepts and enhance the ability to analyze complex pulley systems effectively.
Conclusion
Analysis of systems involving pulleys provides a robust framework for understanding fundamental principles of classical mechanics. Exploration of these systems offers valuable insights into concepts such as force, tension, work, energy, and mechanical advantage. From simple configurations to complex arrangements, the study of pulley mechanics enhances problem-solving skills applicable across various scientific and engineering disciplines. Understanding the interplay of forces, the constraints imposed by interconnected components, and the principles governing energy transformations within these systems equips one with a deeper appreciation for the elegance and power of mechanical principles.
Mastery of pulley mechanics extends beyond theoretical understanding; it empowers practical application in diverse fields, from designing efficient lifting systems to analyzing complex machinery. Continued exploration and rigorous application of these principles are essential for advancements in engineering and problem-solving across a spectrum of scientific endeavors. Further investigation into areas involving friction, non-ideal ropes, and rotational dynamics offers opportunities to refine understanding and tackle real-world challenges with greater precision and insight. The enduring relevance of pulley mechanics underscores its significance as a cornerstone of classical physics and a valuable tool for addressing complex engineering problems.